The resulting data
After reading out and plotting the data, this is what I got. Horizontal is the
sample number, vertical is the AD readout which basically corresponds with
a scale from -6G to +6G.
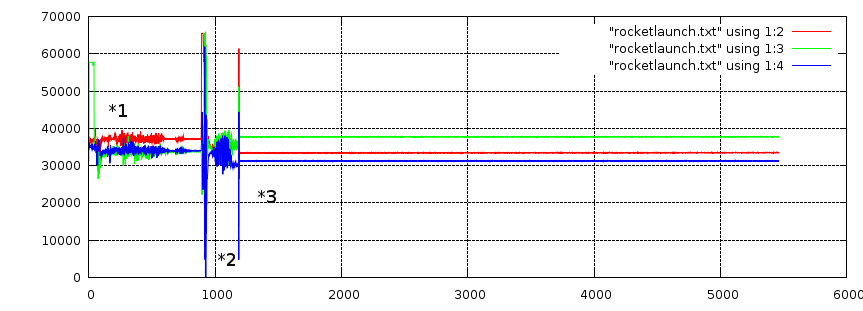
An explanation of what happens: at 1, the rocket is brought to the launching
pad. 2 is the launch, flight and subsequent falldown to earth. 3 is the
nose-cone containing the logger lying still in the mud somewhere, waiting for
us to find it. Only part 2 is really interesting, so let's zoom in on it.
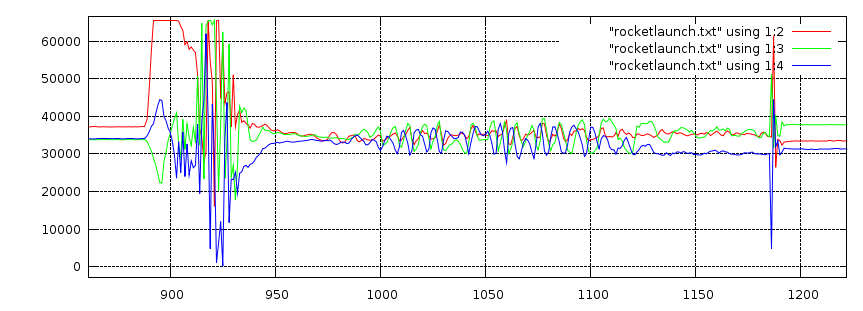
What you can see here is the readout clipping at the 900-samples mark because of
the sheer force at take-off. After that, there seems to be some vibrations,
possibly induced by the airflow, which die out at about 975 samples. Then
the device starts tumbling down to the ground until it finally hits dirt
at 1185 samples.
A quick calibration reveals that the firmware does about 22 samples a second.
This means the rocket took about 3 seconds to reach its apex, while the
process of tumbling down took about 8.5 seconds. While the nose probably
isn't the most aerodynamic thing in the world, we can probably approach the
height it reached by looking at it as a solid, frictionless object falling to
the ground in a time of 8.5 seconds. If my physics knowledge serves me right
(and I do hope it does, it's been a while...) this would mean the rocket
has soared up to a height of 0.5*(8.5sec^2)*9.8=700350 meters (thanks, 'a person'). While the real height
probably is less because the nose-cone would have reached terminal velocity after
a few seconds, it does give a nice indication of the order of
magnitude of height such devices can reach.
If you want to draw your own conclusion from the actual flight data, you can download it here. Offcourse, if you think your estimation of the maximum height is better than mine, feel free to comment.
Last 10 comments Show allThe engine that Sprite used was a D7-3 from "Weco". The rocket itself was made from thick paper (250 g/m2), and was designed and built on site.
Actually the people behind the accelerometer do provide free samples. That company happens to be Freescale. And as it happens the next question is, "What company's rocket engines and kits did you use?"
I think that spike around 41 s' could be the charge that launches the parachute. In the rocket engines I have used there was a small charge at the end. At first it would have to blow the top of the rocket engine and the rocket tip off, pressure initially would go downwards causing thrust. The charge is delayed by a small amount to go off after the engine burnt out. I am not an expert, but I do like my rockets. It appears to be quite possible given that the rocket in question had such a charge.
wow patrick, that's great, didn't think it's possible to extract that much info from it. Anyone explain why the acceleration starts increasing again at ~41.5s?
I took a crack at calibrating the data. I used the fact that the net acceleration measured by the three channels should be 9.8 m/s/s to bang out the cal. I also removed a slowly increasing bias from the data. After I got the cal I used the general shape and peak in the acceleration seen in the y and z channels to guess where the peak in the x acceleration was (why not). I put the work up here: http://www.lobsterharmonica.com/stuff/hackaday_rocket_logger/hackaday_rocket.html There's a link on that page to the calibrated data. I'm too lazy to try and turn it into range right now.
the train, true, some fancy ass accelerometers auto-resole and compensate for the gravity vector. They charge the deflected side of the proof mass and use the e-field charge to move the tuning fork tips back into the center positions, so the sensor has the most dynamic range.
I like the cheap Nunchuck too but on the other hand that chip is $3.50 from digikey, granted no brakeout bourd.
Accelerometers work best when they're at the center of mass of the system. All that laterally directed hash at launch is likely due the nose of the rocket coning around.
pretty sure all accelerometers output 1G in the vertically oriented axis when stationary... because the device is still experiencing 1G of accelleration towards the centre of the earth (gravity)! Just a thought: if you orient the sensor at 45deg, you might be able to calculate a better vertical accelleration from the vector sum of two axes before clipping occurs.
Nice work. I have done the same with MMA7260 and home-made water rockets with bottles (more safe)... The problem is that accelrometer run over the 6G, seems to reach 10G. So have attention on this point when you choose your rocket. Best regards.